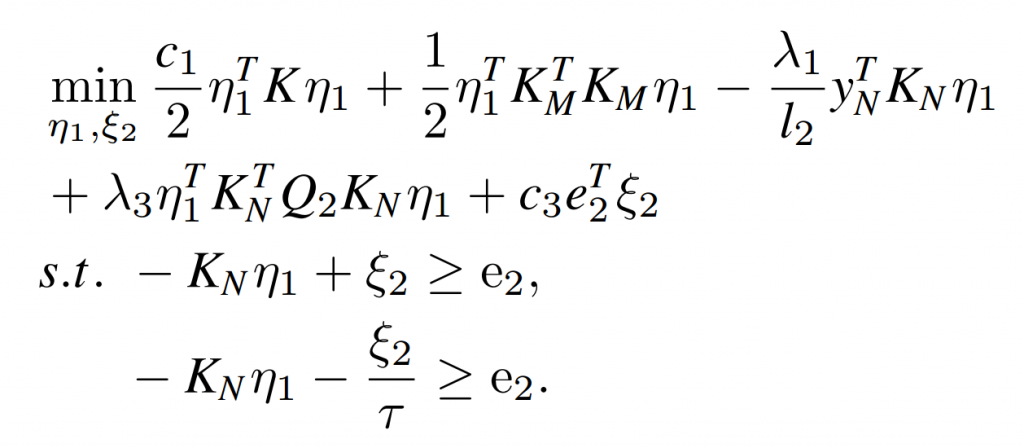机器学习相关数学知识

本文最后更新于405 天前，其中的信息可能已经过时，如有错误请发送邮件到blue16@email.swu.edu.cn

前言

机器学习，又叫统计学习。既然是和数学相关的，肯定要学习相关的数学知识，才能更好地理解各种机器学习算法。这篇文章记录了我在学习机器学习中遇到的部分数学知识以及我对他们的理解。

线性代数

向量、矩阵、张量

向量（Vector）

一维数组，可以理解为矩阵的一维形式，通常用来表示空间中的点或方向。例如，在三维空间中的一个点可以表示为一个三维向量。

矩阵（Matrix）

二维数组，通常用来表示线性变换。例如，一个2×2的矩阵可以表示二维空间中的旋转或缩放。

张量（Tensor）

多维数组，可以表示比矩阵更高维的数据结构。例如，一个三维张量可以用来表示一个彩色图像，其中每个维度分别对应高度、宽度和颜色通道。

矩阵的乘法运算性质

(AB)C=A(BC)
A(B+C)=AB+AC
AB!=BA
IA=A AI=A
A0=0 0A=0
如果 A是一个 m×n 的矩阵，B 是一个 n×p 的矩阵，那么它们的乘积 C=AB 将是一个m×p 的矩阵。这意味着第一个矩阵的列数必须等于第二个矩阵的行数。
c(AB)=(cA)B=A(cB)这说明标量可以分配到矩阵乘法中的任意一个因子上。

矩阵的幂运算

矩阵的分数幂

A^1/2=B相当于找到一个B²使得B²=A

降低矩阵的秩

为什么要降低？

自由度：可以理解为矩阵中能够独立变化的元素的数量。

在实际应用中，降低矩阵的秩通常用于数据压缩、特征选择、信号处理等领域，通过去除冗余信息来简化问题或减少计算量。

见过的降低方法

矩阵乘法

将矩阵与另一个矩阵相乘，如果第二个矩阵的秩小于原始矩阵的秩，那么乘积矩阵的秩也会降低。

矩阵转置的运算规则

矩阵转置有一些基本的性质，比如：

( (A^T)^T = A )，即转置两次矩阵会回到原矩阵。
( (A + B)^T = A^T + B^T )，即两个矩阵相加后转置等于这两个矩阵分别转置后再相加。
( (KA)^T = K(A^T) )，其中( K )是一个常数，表明矩阵乘以常数后转置等于这个常数乘以矩阵转置。
( (AB)^T = B^T A^T )，即两个矩阵相乘后的转置等于第二个矩阵的转置乘以第一个矩阵的转置。

矩阵可逆

矩阵可逆是指一个方阵（即行数和列数相等的矩阵）存在一个逆矩阵，使得这两个矩阵相乘的结果是单位矩阵。单位矩阵是一个主对角线上的元素都是1，而其他位置上的元素都是0的方阵。

具体来说，对于一个给定的n×n方阵A，如果存在另一个n×n方阵B，使得以下等式成立：

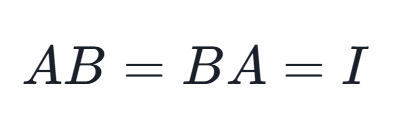
其中II是n×n的单位矩阵，那么我们称矩阵A是可逆的，并且矩阵B被称为A的逆矩阵，通常记作A^-1。

矩阵的迹

定义

迹是指一个方阵（行数与列数相等的矩阵）的主对角线（从左上到右下的线）上所有元素的和。换句话说，迹就是沿着主对角线从左上角到右下角的所有元素的累加和。

迹运算只定义在方阵上。

运算性质

1.线性：对于任意两个 n×n 矩阵 A 和 B，以及任意标量 c，有

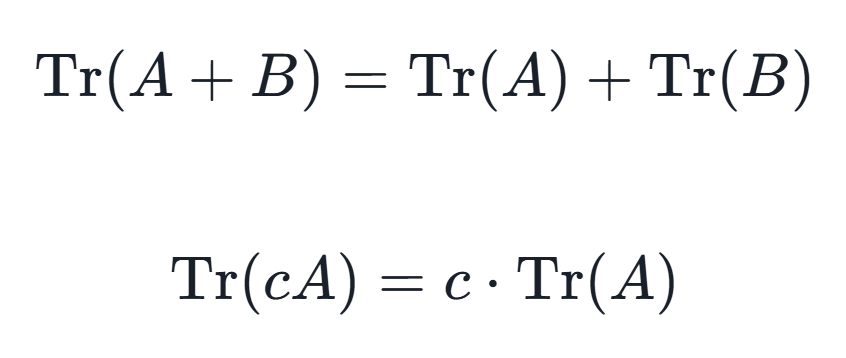
2.循环不变性：对于任意n×n矩阵A和B，有

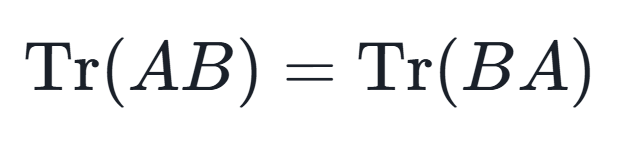
即使 AA 和 BB 不一定是方阵，只要它们的乘积AB和BA有意义，上述性质也成立。

3.对换性：对于任意 n×n矩阵 A，有

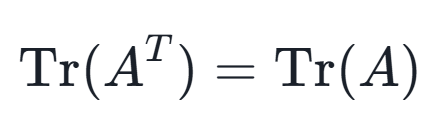
4.迹的循环性质（Cycle Property of Trace）：对于任意的矩阵 A、B 和 C，有：

tr(ABC)=tr(BCA)=tr(CAB)

矩阵奇异/不奇异

等价于说矩阵是否可逆，矩阵奇异意味着矩阵不可逆，矩阵不奇异意味着矩阵可逆。

奇异值分解（singular value decomposition,SVD）

定义

奇异值分解（SVD, Singular Value Decomposition）是一种在矩阵理论中非常重要的线性代数工具，它可以将任意一个m×nm×n的矩阵AA分解为三个矩阵的乘积形式，即：

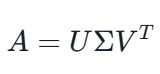
这里的三个矩阵具有以下特性：

U是一个m×m的单位正交矩阵，它的列向量称为左奇异向量，它们构成了矩阵A行空间的一个正交基。
Σ是一个m×n的对角矩阵，但除了主对角线上的元素外，其他位置都是0。主对角线上的非负数称为奇异值，它们按照从大到小的顺序排列，奇异值的数目等于A的秩。奇异值的大小表示了原矩阵A在对应奇异向量方向上的“拉伸”程度。
VT是n×n的单位正交矩阵的转置，其行向量称为右奇异向量，它们构成了矩阵A列空间的一个正交基。

作用

揭示矩阵的内在结构，通过分解可以更好地理解矩阵的性质和行为。

奇异值阈值算子（singular value thresholding，SVT）

还在研究…

矩阵的秩

定义

矩阵的秩就是矩阵中非零子式的最高阶数。

矩阵的秩是指矩阵中线性无关的行（或列）的最大数目，它是一个非常重要的矩阵特征，可以用来描述矩阵的“大小”或者“复杂度”。

矩阵范数

矩阵范数（matrix norm）是数学上向量范数对矩阵的一个自然推广。

范数(norm)：范数是一种在数学和物理学中用来衡量向量“大小”或者“长度”的函数。更一般地，它可以用来衡量函数、序列、算子等数学对象的“大小”。在不同的数学分支中，范数的定义和性质可能有所不同，但它们都有一些共同的基本特征。

正则化

正则化是一种在机器学习和统计学习中对模型进行优化的方法，旨在防止模型在训练数据上过度拟合（overfitting）。过度拟合是指模型对训练数据学得“太好”，以至于它捕捉到了数据中的噪声而不是潜在的模式，导致模型在新的、未见过的数据上表现不佳。
正则化的主要目的是通过以下几种方式来提高模型的泛化能力：

惩罚复杂模型：通过给模型的复杂度添加惩罚项，鼓励模型选择参数值较小的解，从而简化模型结构。
控制模型权重：正则化通过限制权重的大小，使得模型不会对训练数据中的随机噪声做出强烈反应。
常见的正则化方法包括：

L1正则化（Lasso回归）：在损失函数中添加权重的绝对值和的惩罚项。这可能导致某些权重为零，从而实现特征的自动选择。
L2正则化（Ridge回归）：在损失函数中添加权重的平方和的惩罚项。这会使权重尽量小，但不会变成零。
弹性网（Elastic Net）：是L1和L2正则化的组合，通过一个参数控制两者之间的平衡。
Dropout：在训练神经网络时，随机地“丢弃”（即设置输出为零）一些神经元及其连接，以减少模型对特定训练样本的依赖。
数据增强：在训练过程中对数据进行变换，人为地扩大训练集的规模，以防止模型记住训练样本。
正则化是提高机器学习模型泛化能力的重要技术，它帮助确保模型能够在实际应用中更好地工作。在设计模型时，选择合适的正则化方法对于获得一个既精确又鲁棒的模型至关重要。

矩阵的迹(trace)

在线性代数中，tr(A)表示矩阵A的迹（trace）。迹是一个方阵的所有对角线元素之和。具体来说，如果A是一个n×n的矩阵，那么它的迹就是A的第1行第1列、第2行第2列、……、第n行第n列元素的和，用数学公式表示就是：

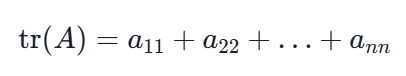
最优化相关

拉格朗日乘数法

拉格朗日乘数法：

机器学习知识点总结 – 拉格朗日乘子法（Lagrange Multiplier Method）详解-CSDN博客

凸优化问题的定义

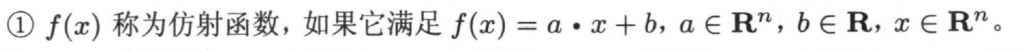
凸二次规划问题 (QPP,Quadratic programming problem)

目标函数是二次，约束条件是线性=> 凸二次规划问题 (QPP,Quadratic programming problem)，理想情况可以使用一些QP的套件直接进行求解得到答案，但是存在样本维度过高或者样本数很多，或者存在样本特征升维的一些情况，QP可能就不太能够直接求解，由此引入了对偶求解的概念。

KKT条件

参考文章：KKT条件，原来如此简单 (上) | 理论部分 – 知乎 (zhihu.com)

KKT条件(Karush–Kuhn–Tucker conditions)是最优化（特别是非线性规划）领域最重要的成果之一，是判断某点是极值点的必要条件。

对偶理论

Wolfe对偶

dual form

前言