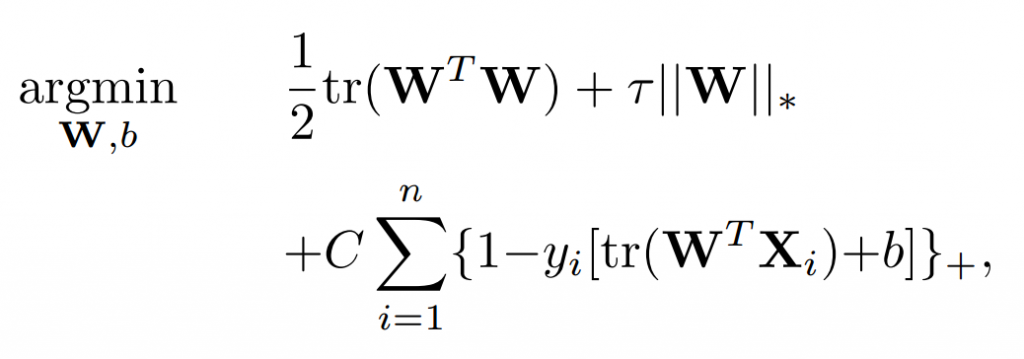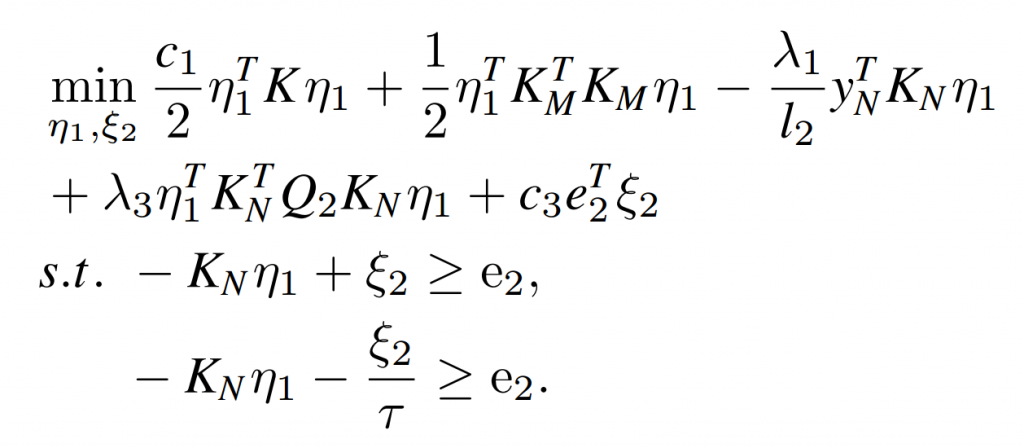问题背景

脑电图、图像分类：输入的信息是矩阵。传统的支持向量机：会忽略结构信息。

为了利用这种结构信息，我们提出一种新的分类方法，我们称之为支持矩阵机(SMM)

SMM = Hinge Loss + spectral elastic net penalty

SMM问题：凸优化->采用ADMM算法

介绍

核心：试图利用数据矩阵的列或行之间的相关性（利用结构信息）。

Wolf et al (2007) proposed a rank-k SVM, which models the regression matrix as the sum of k rank-one orthogonal matrices. Pirsiavash et al (2009) devised a bilinear SVM by factorizing the regression matrix into two lowrank matrices. Cai et al (2006) proposed a similar bilinear framework called support tensor machines for text categorization.

之前的研究：rank-k SVM、

导致的问题：非凸优化问题

本篇论文的模型的创新点：

First, we consider the hinge loss due to its widely deployed ability in sparseness and robustness modeling. Second, we employ a spectral elastic net penalty for the regression matrix.

• 损失函数：hinge loss
• 惩罚项：spectral elastic net penalty（传统的：elastic net）

三种范数

弗罗贝尼乌斯范数（Frobenius norm）

有点类似于我们常见的距离的计算方法：平方开根号

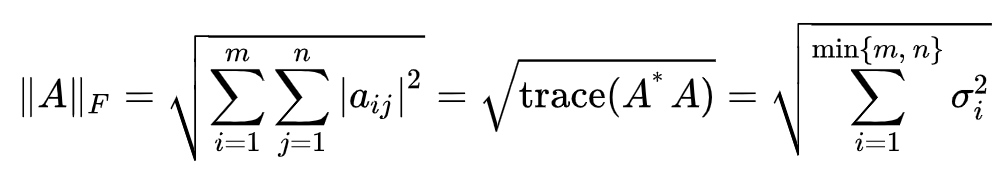
核范数（Nuclear norm）

就是矩阵在奇异值分解（SVD）中矩阵Σ对角线上所有奇异值的和：

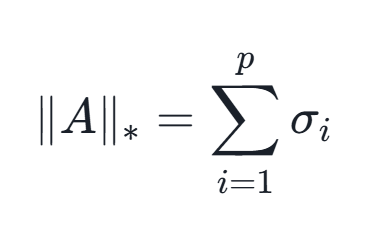
谱范数（Spectral norm）

矩阵的最大奇异值。

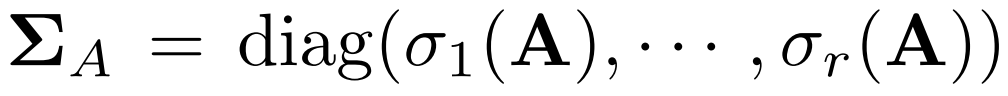
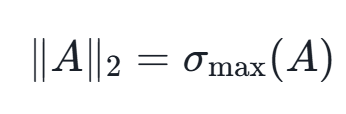
支持矩阵机(SMM)