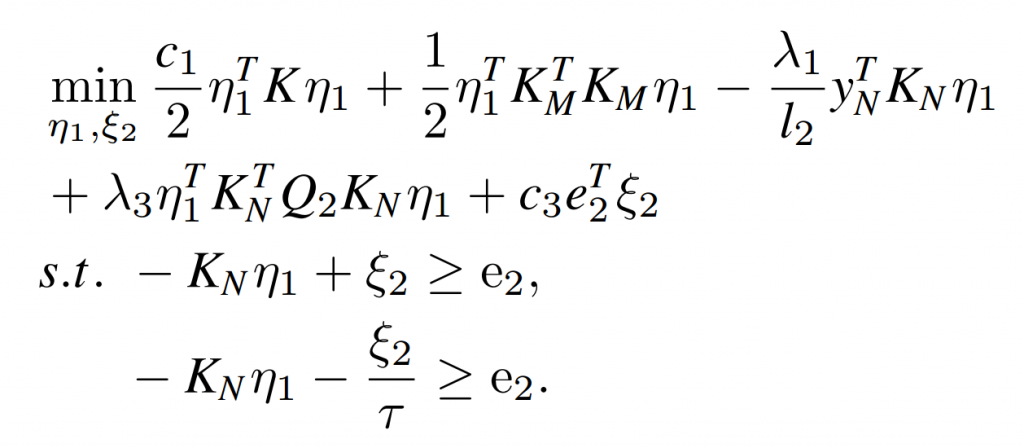简介
我们描述了一种学习双线性支持向量机的算法。双线性分类器是双线性模型的判别变体,它捕捉数据对多个因素的依赖性。这种模型特别适合于用矩阵(matrix)或张量(tensor)而不是向量(vector)表示的可视化数据。矩阵编码允许通过秩限制进行更自然的正则化。
模型推导
线性预测模型的展现形式(这里w和x均为列向量):
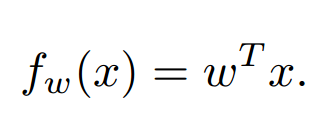
将该公式推广到矩阵形式:
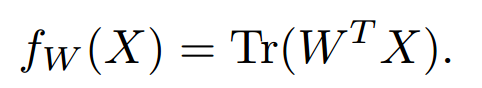
Tips:为什么是这个?这种表示形式确保了X中每一个元素与一个w相乘(非主对角线的元素都被舍弃了),相当于转为了一个线性的预测模型。
为了降低矩阵自由度,方便学习,通过乘法的方式降低矩阵的秩(x方向的投影和y方向的投影的秩取最小):
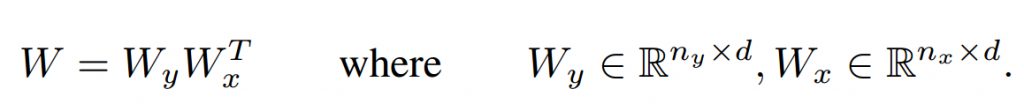
带入到上面的公式,最终的公式为:
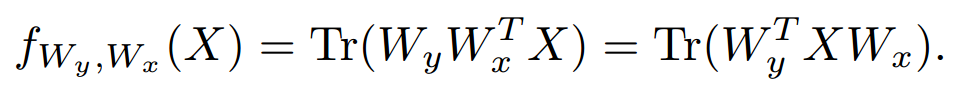
类比于SVM的经典模型(Hinge loss,前者),提出新的模型(后者):
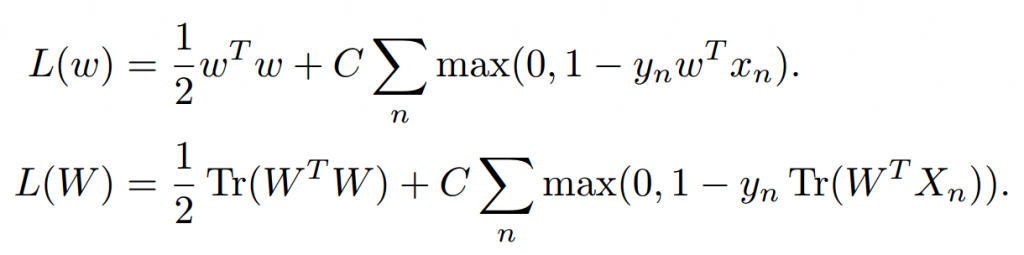
- Tips:Tr(WTW)的含义是把所有元素平方求和(非主对角线的元素都被舍弃了,恰好是相同的元素乘相同的元素),相当于SVM中的求范数的平方了。
可以证明(怎么证明的?),这两个都是凸优化问题。
- Tips:这两个公式长得很类似,其实推一下就发现是完全一样的(会操作矩阵每一个元素),因此可以用常规的SVM优化器。
降低W的秩(带入之前通过矩阵乘法降秩的公式),得出如下目标函数:
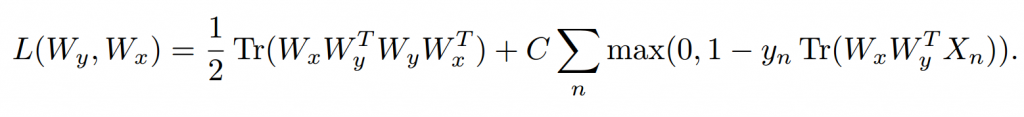
可以证明(怎么证明的?),这个问题为一个双凸优化问题(biconvex)。
优化算法
坐标下降(Coordinate descent)
We can optimize (7) with a coordinate descent algorithm that solves for one set of parameters holding the other fixed. Each step in this descent is a convex optimization that can be solved with a standard SVM solver.
也就是说,通过固定参数的方式,把这个问题的每一步转为一个凸优化问题,这个凸优化问题就能够用常规SVM求解器进行求解。
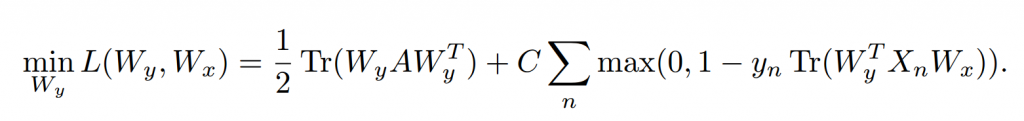
Tips:这里是怎么固定的?其实是用了乘法的结合律和对称性,先推出与x相关的,自然就能到到与y相关的。

为了解决这个问题,我们要把上面的式子转为上面说的凸优化问题:
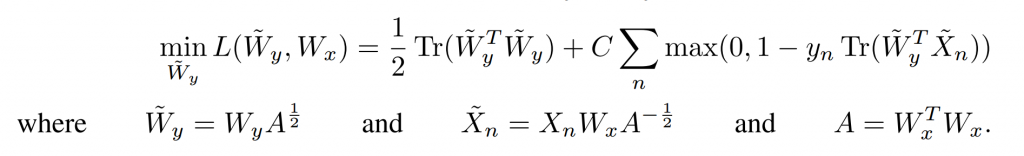
- Tips:这里A是对称矩,A和它的转置是相等的。